Effects of canard wing interference on the flight characteristics of a civilian transonic cruiser are examined. The aircraft is an unconventional design concept with no historical data. The flight characteristics of the aircraft are predicted using aerodynamic models in the form of look-up tables, generated using high-fidelity computational fluid dynamics simulations and a potential ow solver. These tables contain longitudinal and lateral force and moment coefficients for different combinations of angle of attack, side-slip angle, and control surface deflections. Dynamic damping derivatives are calculated from time-accurate simulations of the aircraft models oscillating in pitch, roll, and yaw direction and using a linear regression estimation method. The static simulations are performed at a Mach number of 0.117, as reported in wind tunnel experiments, and for two different canard positions using an overset grid approach. The aerodynamic tables include canard deflections of [-30, -10, 0, 10] at angles of attack from -4 to 30 degrees. Lateral coefficients are simulated at sideslip angles of -6 and 6 degrees as well. The dynamic simulations are performed for aircraft oscillations about mean angles of attack between zero to ten degrees with a motion frequency of 1Hz and amplitude of 0.5 degrees. The predicted aerodynamic data are then compared with those measured in wind tunnel experiments and calculated from the potential ow solver. The results show that both static and dynamic predictions match reasonably well with experiments for the range of angles considered.
In the present study, the effects of different canard configurations on the flight characteristics of a transonic passenger aircraft concept is examined. This design concept, named the TransCRuiser (TCR), was proposed by the Swedish aerospace company SAAB and was studied using in-house design procedures at SAAB. Since then, the design has undergone several design changes including the addition of a front canard to improve the aircraft handling qualities in particular during a European project named SimSAC The addition of a canard provides a secondary lifting surface that could make the aircraft stall-proof, since the canard will stall before the main wing. This induces a pitching moment on the aircraft, thus reducing its angle of attack until the canard begins to generate lift again. However, the canard also tends to reduce the stability of the aircraft when compared to conventional designs.
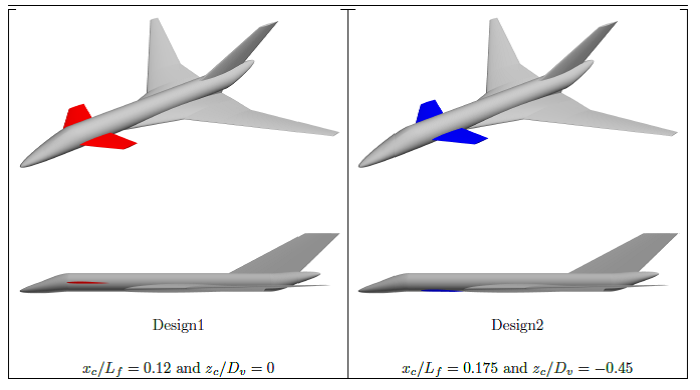
The original TCR model has a canard positioned at 0.12 of total fuselage length and at the mid fuselage section. This is named “Design1” in this paper. A second design (named “Design2”) is considered as well that has canard positioned at 0.175 of total fuselage length and at a lower position than the original design.
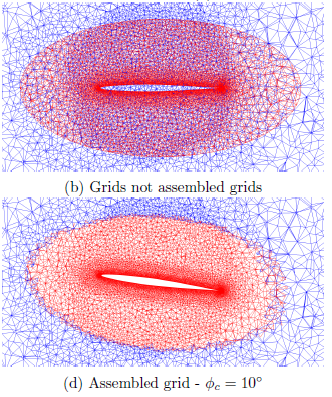
For the grids, a background viscous mesh was created around the fuselage, wing, and the tail. The canard viscous grids (right and left) were generated individually as well. The canard grids are then overset to the background mesh as illustrated below. Right- and left-side canard grids have fringe boundary surfaces (FBSs) that transfer information between grids. The overset grid module in Cobalt then performs an automatic hole cutting by interpolating FBS in each grid. The hole cutting process can be seen in below. Each canard (minor) grid contains about six million cells while the background grid has about 60 million cells. The assembled grid has about 70 million cells.
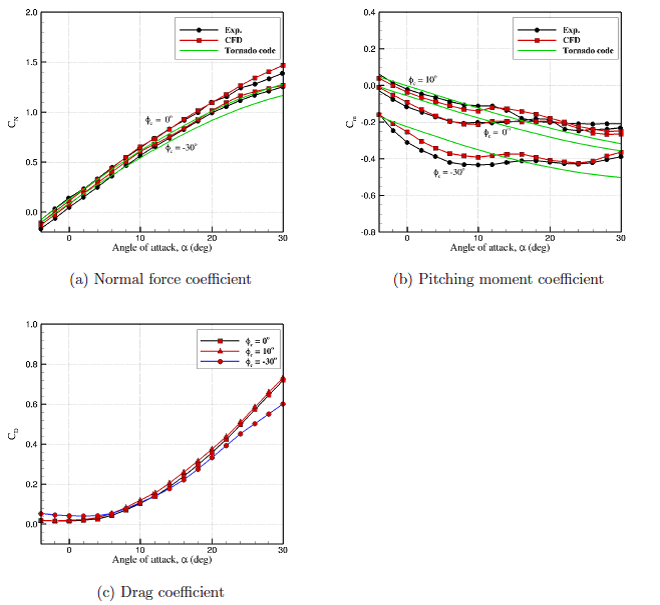
Longitudinal aerodynamic predictions of TCR-Design1 using CFD and Tornado code are shown below and compared with wind tunnel measurements. The figure shows that CFD data closely match with experiments at almost all angles of attack. TCR-Design1 shows no sign of stall in the range of angles of attack presented. However, the aerodynamic data are highly nonlinear in particular at moderate to high angles of attack. For example, both CFD and experiment show a negative slope pitching moment at small angles of attack. At about eight to ten degrees angle of attack, the pitching moment slope becomes zero and even positive. For a zero canard deflection, the pitching moment slope again becomes negative about 20 degrees angle of attack. The figure shows that a positive canard deflection increases normal force and pitching moment. The drag will also become higher than non-deflected canard at high angles of attack.
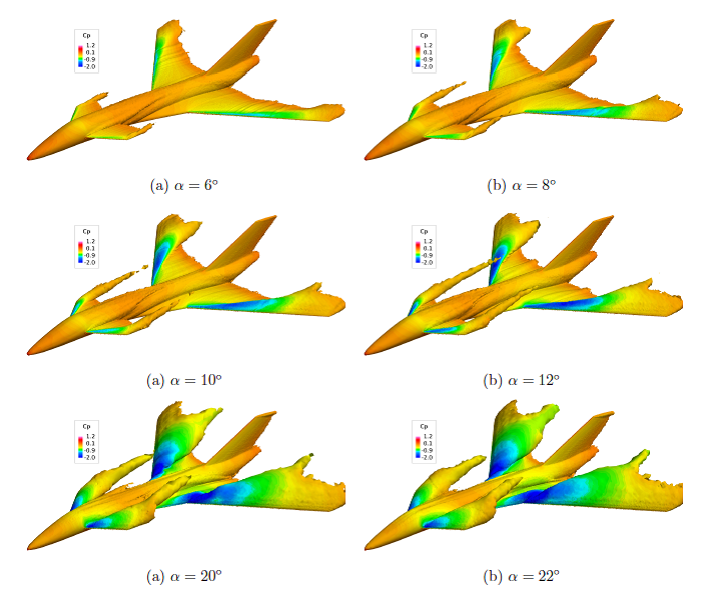
Some flow features of TCR-Design1 are presented below in which vorticity isosurfaces are colored by pressure coefficient. The image below shows tip vortices formed at six degrees angle of attack. At α= 8°, a vortex is formed over the wing, however, the vortex starting point is not at the wing apex. This vortex induces negative pressures over the surface and causes the lift to increase. At higher angles of attack, the vortex starting point moves toward the wing apex which causes a positive increment in the pitching moment. At α = 10°, the vortex starting point is at the wing apex. The canard vortex can be seen at this angle. Further increase in the angle of attack does not move the vortex starting point, but vortices become stronger and larger in size. At about α = 20°, the canard vortex lifts up from the surface and the canard lift suddenly drops causing more changes in the pitching moment slopes.
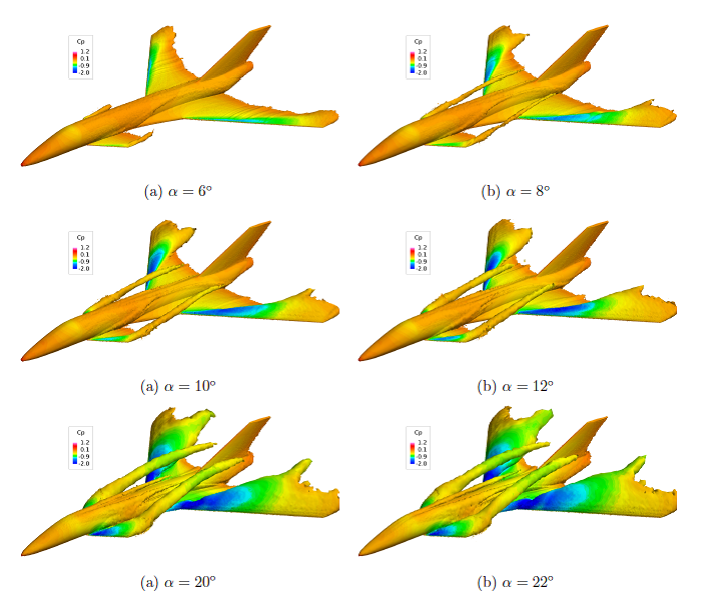
Finally, some of the flow features of TCR-Design2 are shown in the images below. The flow structures are similar to those found in Design-1, except that the aft-positioned canard has stronger canard vortices.
This work presented the canard wing interference e ects on the ight characteristics of a civilian transonic cruiser. The low speed aerodynamic characteristics of the TCR are available from the SimSAC project and were used in this work to validate CFD predictions. All tests were run at a free-stream velocity of 40 m/s, which corresponds to a sea level Mach number of 0.117, and a Reynolds number of 0.778 million based on the mean aerodynamic chord of the wind tunnel model.
For further information, you can read the full paper, Canard-Wing Interference Effects on the Flight Characteristics of a Transonic Passenger Aircraft, by Harrison, Darragh, Hamlington, Ghoreyshi and Lofthouse